
1.1 벡터
벡터(vector)는 크기와 방향을 가진 수량(quantity)을 가리키는 말이다. 벡터는 힘이나 변위, 그리고 속도를 나타내는 데 쓰인다. 벡터를 기하학적으로 방향이 있는 선분, 지향 선분(directed line segment)으로 표시한다. 선분의 길이는 벡터의 크기를, 선분 끝의 화살표는 벡터의 방향을 나타낸다. 길이가 같고 같은 방향을 가리키는 벡터는 서로 같은 벡터이다.
1.1.1 벡터와 좌표계
벡터를 그 꼬리가 3차원 좌표계의 원점과 일치하도록 이동하면 벡터 v를 (x, y, z)로 표기할 수 있다. 이렇게 3차원 벡터를 컴퓨터 프로그램 안에서 세 부동소수점(float, double)으로 표현할 수 있다.
참고 기준계(frame of reference), 공간(space) 그리고 좌표계(coordinate system)는 모두 같은 말이다.
같은 벡터라도 기준계가 다르면 그 좌표 표현이 달라진다. 즉, 어떤 벡터를 좌표로 규정하거나 식별할 때 좌표계에 따라서 상대적으로 나타낼 수 있다. 3차원 컴퓨터 그래픽에서는 다양한 기준계를 사용하는 경우가 많으므로 현재 어떤 기준계가 기준인지 기억할 필요가 있다.
1.1.2 왼손잡이 좌표계와 오른손잡이 좌표계
Direct3D는 왼손잡이 좌표계(left-handed coordinate system)를 사용한다.

1.1.3 기본적인 벡터 연산
u = (ux, uy, uz), v = (vx, vy, vz)일 때 벡터의 상등, 덧셈, 뺄셈, 그리고 스칼라 곱셈을 정의해 보자.
- ux = vx, uy = vy, uz = vz일 때, u = v이다.
- u + v = (ux + vx, uy + vy, uz + vz)이다.
- u - v = (ux - vx, uy - vy, uz - vz)이다.
- k를 스칼라라고 할 때, ku = (k * ux, k * uy, k * uz)이다.
1.2 길이와 단위 벡터
기하학적으로 한 벡터의 크기는 해당 지향 선분의 길이이다. 벡터 u = (x, y, z)가 주어졌을 때, u의 크기(길이)는 ||u||으로 표기한다. 벡터를 방향을 나타내는 용도로 사용할 경우, 크기가 1인 단위 벡터(unit vector)로 주로 표현한다. 어떤 벡터를 단위 벡터로 변환하는 것을 정규화(normalization)라고 한다.

1.3 내적
내적(inner product, dot product)은 스칼라 값을 내는 곱셈의 일종으로 u = (ux, uy, uz), v = (vx, vy, vz)라고 할 때, 내적은 다음과 같이 정의한다. 이때 θ는 u와 v 사이의 0 ≤ θ ≤ π를 만족하는 각도이다.
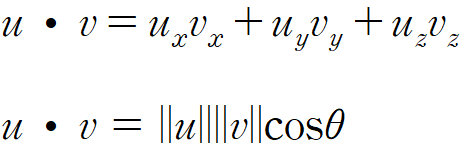
- u·v = 0이면 두 벡터 u, v는 직교한다.
- u·v > 0이면 두 벡터 사이의 각도 θ는 90도보다 작다, 즉 예각이다.
- u·v < 0이면 두 벡터 사이의 각도 θ는 90도보다 크다, 즉 둔각이다.
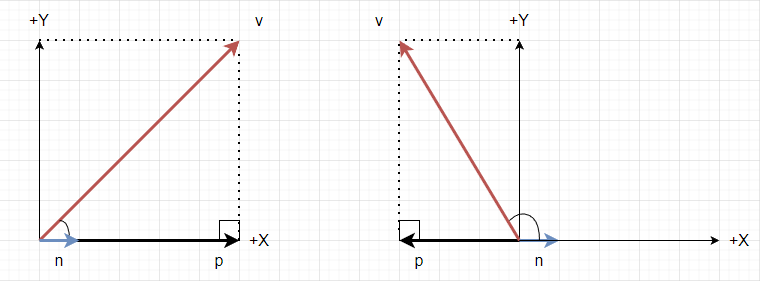
벡터 v와 벡터 n이 주어졌을 때, p를 내적을 이용해서 v와 n으로 다음과 같이 표현할 수 있다. 이러한 p를 n에 대한 v의 직교 투영(orthographic projection; 혹은 정사영)이라고 부른다.
- p = projn(v) = (v·n) / ||n||^2 × n
1.3.1 내적을 이용한 직교화
벡터 집합 {v0, v1, ..., vn-1}의 모든 벡터가 단위 길이이고 서로 직교일 때, 그러한 벡터 집합을 정규직교(orthonormal) 집합이라고 부른다. 정규직교가 아닌 벡터 집합을 정규직교 집합으로 만드는 것을 직교화(orthogonalization)라고 한다. n개의 벡터들의 집합을 정규직교 집합으로 직교화할 때 그람-슈미트 직교화라고 하는 공정을 적용한다.
1.4 외적
외적(outer product, cross product)은 벡터를 결과로 내는 곱셈의 일종으로, 두 3차원 벡터 u와 v의 외적을 취하면 u와 v 모두에 직교인 또 다른 벡터 w가 나온다. u = (ux, uy, uz), v = (vx, vy, vz)라고 할 때, 외적은 다음과 같이 정의한다.

1.4.1 외적을 이용한 직교화
벡터 집합 {v0, v1, v2}를 직교화하는 또 다른 공정은 외적을 이용한 직교화이다.


1.5 점
특정한 좌표계를 기준으로 표준 위치에 있는 어떤 벡터를 3차원 공간 안의 한 위치를 나타내는 데 사용할 수 있는데, 이를 위치 벡터라고 한다. 위치 벡터는 그 크기가 방향이 아니라 벡터 머리의 좌표에 의미가 있다. 위치 벡터, 즉 점에 대해 의미 있는 벡터 연산은 두 점의 차 q - p와 점 p 더하기 벡터 v이다.

- 두 점의 차 q - p는 p에서 q로 가는 벡터이다.
- 점 p 더하기 벡터 v는 p의 위치를 v만큼 옮겼을 때 도달하는 점이다.
'Computer Science > 컴퓨터 그래픽스' 카테고리의 다른 글
| 3D 게임 프로그래밍 | Part 02 실시간 파이프라인 | Chapter 02 렌더링 파이프라인 (0) | 2023.03.29 |
|---|---|
| 3D 게임 프로그래밍 | Part 02 실시간 파이프라인 | Chapter 01 레스터화 (0) | 2023.03.13 |
| 3D 게임 프로그래밍 | Part 01 렌더링 기초 | Chapter 02 광 추적(하) (0) | 2023.02.27 |
| 3D 게임 프로그래밍 | Part 01 렌더링 기초 | Chapter 02 광 추적(상) (0) | 2023.02.27 |
| 3D 게임 프로그래밍 | Part 01 렌더링 기초 | Chapter 01 블룸 효과 (0) | 2023.02.24 |
댓글